A deeper dive into biostatistics: fixed-effect and random-effects models in meta-analysis
BY DR JENS CHAPMAN

In our era of being able to use increasingly large data bases to improve insights into medical conditions and treatments, systematic reviews and—condensed from there—meta-analysis have become a mainstay. The methodology which uses pooled larger data analyses compiled from several studies was introduced over 30 years ago in psychiatric literature and is becoming more and more widely used also in all clinical research.
A recent Science in Spine article in Global Spine Journal comparing fixed-effect and random-effects models for meta-analysis received a lot of attention. In this brief, I wanted to delve into the subject matter of what to look for in meta-analyses in greater but less technical detail as some caution seems to be appropriate when looking at this statistical methodology.
Disclaimer: The article represents the opinion of individual authors exclusively and not necessarily the opinion of AO or its clinical specialties.
For starters, a meta-analysis is the statistical procedure for combining data from multiple studies, but it does not, as is commonly believed, simply pool data from a number of smaller studies into one large one. Instead, meta-analysis should also use a number of statistical methods that take into account the differences in the sample sizes of each study as well as the differences (heterogeneity) between each study’s approach and its findings.
Meta-analyses have become so popular compared to single studies as they can amplify research impact through enhanced statistical power and reporting accuracy and ideally conclude with a clinically useful summary of findings. Frequently, meta-analyses can even help arbitrage divergent study and converge towards one overarching conclusion where individual smaller studies had remained inconclusive.
Some caution should be applied when looking at a meta-analysis—and hence this more expansive reflection on our previous article. To conduct a metanalysis is not a magical process that will provide conclusive incontestable results as it ultimately relies on the quality of the included studies themselves—with factors such as sample size and framing of eligibility criteria looming large. Most importantly perhaps, metanalyses requires an understanding of the statistical models that underlie the analysis.
Most meta-analyses are based on one of two statistical models: either a fixed-effect model or the random-effects model. Both terms refer to the effect size, a concept that measures the relationship between two variables on a numeric scale. For example, different studies may show that men are generally taller than women—and so the greater the difference in height in each study, the greater the effect size. By looking at the effect size in each study, you can determine whether the difference is real, or whether it could be due to other factors such as demographics, geography, education, or a variety of other possibly relevant pre-existing conditions.
So, when it comes looking at a meta-analysis, the point of our article was to be aware of the difference between fixed-effect and random-effects models as this will influence any eventual results and therefore conclusions.
Fixed effect vs random effects
The fixed-effect model assumes one true effect size underlies all the studies in the meta-analysis, thus the term “fixed effect”. Therefore, any differences in observed effects are assumed to be due to sampling errors.
The random-effects model instead acknowledges that the true effect could vary from study to study due to a number of inherent differences among various studies. For example, the effect size might be higher or lower in trials where the participants’ demographics vary (older versus younger, lower versus higher socio-economic status, or less versus higher educated), or when a different surgical is applied. This is particularly relevant for clinical studies that combine data from diverse socio-cultural back grounds and health care systems, for instance where the same type of surgery is performed as an outpatient surgery versus a several-day hospital inpatient stay. In this example this insight is important as this variable is part of the cultural expectation of that particular part of the world and the length of stay therefore is not an immediately applicable measurement tool of a surgical quality of care.
As studies will also frequently differ in the composition of its participants and in the implementation of surgical interventions, (among other reasons), each study may have a different effect size. If it were possible to perform an infinite number of studies, the effect estimates of all the studies would follow a normal distribution. The pooled estimate would be the mean or average effect. The effect sizes in the studies that are performed are assumed to represent a random sample of all possible effect sizes, hence the term “random effects”. Investigators use the plural ‘effects’ since there is a range of true effects.
The statistics for fixed-effect and random-effects models are different
We know that in a meta-analysis, a pooled estimate is calculated as a weighted average of the effect estimates within the individual studies. Weights are assigned to each study based on the inverse of the overall error variance (ie, 1/variance). Generally, more weight is assigned to studies with larger sample sizes.
In the fixed-effect model, all observed differences reflect sampling error. Therefore, any variance would come from within each study. The pooled estimate is calculated as a weighted average, where the weight assigned to each study is the inverse of that study’s variance. Larger studies have much more weight than smaller studies in the fixed-effect models. Well known methods used for fixed-effect model assessments include the ‘Peto odds ratio’ and the ‘Mantel-Haenszel’ method.
In the random-effects model, two sources contribute to the variance—one which arises from within each study, and another variance that is present between different studies. Both sources of variations should really be taken into account. While larger studies still have larger weights, in the random effects models, smaller studies will be assigned relatively greater weight than fixed-effect models. The method frequently used to account for both sources of variance is the ‘DerSimonian and Laird’ method.
The results under each model may be similar or different
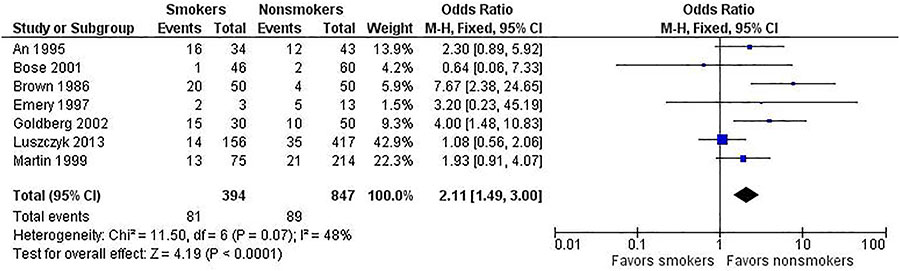
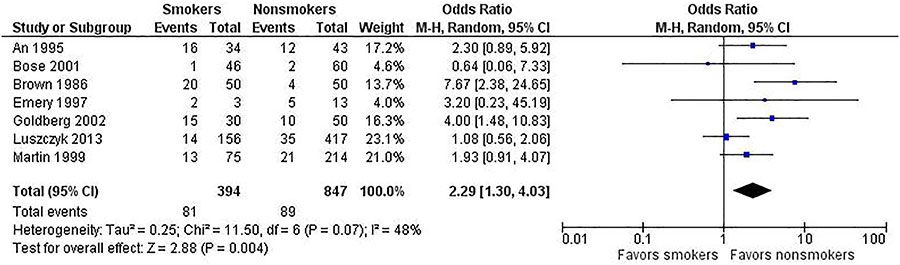
To help illustrate this point, let’s use selective data from a meta-analysis on the risk of non-union in smokers undergoing spinal fusion. We present the same data for the fixed-effect (shown in Figure 2) and random-effects (see Figure 3) models to underscore how the different analyses affect the results. Note the following differences.
- The study weights listed in the meta-analysis table and represented by the size of each study’s point estimate are more similar under the random-effects model. Specifically, note the size of the boxes for the largest study (Luszczyk 2013) vs the smallest study (Emery 1997) under the two models.
- The estimate of the effect size differs between the two models. In this case, the random-effects model results in a larger effect size (2.39) than in the fixed-effect model (2.11). The results generated from fixed-effect and random-effects models can be the same or different, with either model yielding a higher estimate of the effect size.
- The confidence interval (the degree of uncertainty around an estimate) for the summary effect is wider under the random-effects model. This will always be the case because the model accounts for two sources of variation.
Ultimately, which model to use depends on the circumstances. Generally, the random-effects model is often the more appropriate model, as it does capture uncertainty resulting from heterogeneity among studies.
When there are too few studies to obtain an accurate estimate of the between-studies variance, the fixed-effect model remains very appropriate. For instance, in the scenario of a researcher being limited to a high-quality study with a large sample size and a low-quality study with a small sample size, a fixed-effect model will assign a greater weight to the larger, better-quality study.
Ultimately, conclusions that can be derived from meta-analyses are very much reliant on the source quality of the studies included. By itself, a meta-analysis can most certainly not compensate for poorly designed studies that meet inclusion criteriae.
Therefore, it is not an uncommon finding that authors describe the level of evidence as ‘weak’ and call for more, better quality research to be able to better answer the question at hand. While not the conclusion one would hope for an honest status check of the quality of available scientific literature can present an important finding in itself.
When, however, existing studies show prove themselves to be well-designed and credible, applying the preferred statistical model for the analysis of collated results is necessary in order to reach the methodologically correct conclusion. I hope that this deeper foray into the wonderful and growing world of metanalyses was helpful to the reader.
About the author
Jens R Chapman MD is a Spine surgeon at the Swedish Neuroscience Institute at the Swedish Medical Center in Seattle, Washington. He serves as a Clinical Professor of Orthopaedic surgery at the WSU Elson S. Floyd Medical School and previously was affiliated with UW Medicine-University of Washington Medical Center and UW Medicine-Harborview Medical Center. He received his medical degree from Technical University Munich Faculty of Medicine and has been in practice for more than 30 years. He has expertise in treating a wide variety of spine conditions including degenerative conditions, dysplasias and deformities as well as Spinal Oncology and traumatic conditions.
Dr Chapman wishes to acknowledge the collaboration with Drs Daniel C Norvell and Joseph Detorri for their in-depth insights in all things Epidemiology.
References and further reading:
- Joseph R. Dettori, Daniel C. Norvell, Jens R. Chapman. Fixed-Effect vs Random-Effects Models for Meta-Analysis: 3 Points to Consider. Global Spine J. 2022: 12(7) 1624-1626.
- Borenstein M, Hedges LV, Higgins JP, Rothstein HR. A basic introduction to fixed-effect and random-effects models for meta-analysis. Res Synth Methods. 2010;1(2):97-111.
- Nunna RS, Ostrov PB, Ansari D, et al. The Risk of Nonunion in Smokers Revisited: A Systematic Review and Meta-Analysis. Global Spine J. 2022;12(3):526-539.
- Dettori JR, Norvell DC, Chapman JR. Seeing the Forest by Looking at the Trees: How to Interpret a Meta-Analysis Forest Plot. Global Spine J. 2021;11(4):614-616.
- OrthoEvidence. Fixed- vs. Random-Effects Models: 5 Tips to Get a Better Understanding. OE Original. 2019;2(112). Available from: https://myorthoevidence.com/Blog/Show/48
You might also be interested in:
Global Spine Journal
The Impact Factor of AO Spine’s official scientific journal goes up to 2.6.
AO Spine Knowledge Forums
The engines of our clinical research, creating new knowledge to make your patients and practice flourish.